豁出去了，二叉搜索树最强学习攻略！

欧清辣哨 · 发表于 2020-8-7 17:27:18

1、我想深入的学习

2、想给大家讲明白，让大家也深入学习

二叉搜索树

为啥要学习二叉搜索树

今天咱们要说的是二叉搜索树，在学习这个之前，建议之前还没有看过我写的树和二叉树的朋友一定要去看看再来！否则你会有点晕乎。

这里先给大家伙普及一下，想必有些人不太清楚，我们之前讲了什么是树，然后接着说了二叉树，这里为啥开始说二叉搜索树了？

说到树这个数据结构，其实蛮重要的，你肯定听说过红黑树，因为jdk1.8中的hashmap就是数组加链表加红黑树，然后你肯定还听过AVL树，是不是听着就感觉高大上，然后学数据库MySQL索引的时候，你一定会接触B树，对还有B+树，同样的高大上（其实还有B-树）

如果你之前不了解，看到这些有种被劝退的感觉，我这里简单先给梳理一下，以后咱们都会详细讲解的：

“其实很多高深的东西都是在原有基础之上发展而来，我们最开始学习树，了解了啥是树，然后开始对树做一些规定，然后产生了二叉树来应用于某些特定的场景，然后我们对二叉树再给定一些要求，然后产生了二叉搜索树，在使用二叉搜索树的过程中发现了一些问题，然后优化优化，再加一些新规定，就产生了AVL树，AVL树主要解决的就是二叉搜索树的平衡问题，然后在AVL树的基础上再优化设计，又出来了红黑树，也就是说，红黑树也是一种平衡二叉搜索树，主语B树也是在原有基础的树之上发展而来的一种结构，进而有B+和B-”

不知道上面说的那些你明白了不，总结一下就是：

1、这些看起来各式各样的树都是一步步发展而来的，我们应该寻根溯源，从最开始的一步步来学习

2、这些都属于高级数据结构，都有一些特定的应用场景，是我们需要格外注意的

也就是说，我们想要学习AVL树和红黑树这些就要先知道啥是二叉搜索树，然后你就会接触二叉搜索树的平衡问题，自然过渡到红黑树这种。

二叉搜索树是个啥

首先，我们必须搞清楚二叉搜索树是个啥？第一点，肯定的那就是它一定是树结构，也就是说二叉搜索树是基本的基础数据结构，看清楚了：

二叉搜索树是基础数据结构，不是什么算法

它是在原有二叉树上增加一些规则从而形成的，也就是本来人家是个二叉树，然后再给它指定一些规则，加了这些规则之后，它就不同于一般的二叉树了，人家有了新名字，就叫做二叉搜索树

那加了人什么规则呢？二叉搜索树有如下规定：

若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
若任意节点的右子树不空，则右子树上所有节点的值均大于或等于它的根节点的值；
任意节点的左、右子树也分别为二叉查找树；

不知道你是否看明白了？我来结合图看看：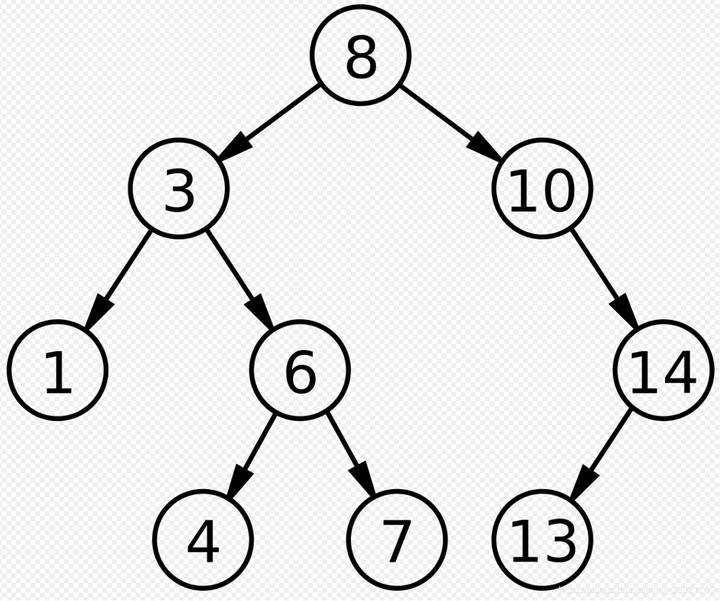

这就是一棵二叉搜索树，然后我们来一次解读它的三条规则：

1、比如8是根节点，左子树不为空，左子树上所有节点的值均小于8，你看看是不是，也就是说这个8左边的树都比它小

2、同样的，这个8的右子树上的所有节点的值都比8大

3、然后每个节点的左右子树也满足上述1和2两条

我一般是这样理解的：

你看啊，我们这里以每一个节点来叙述对象来说，也就是比左边的都大，比右边的都小，这里要记住我们针对的是某一个节点来说，比如我们拿8这个根节点来说，这个8是不是比它左边的数都要大，但是比它右边的数都小

不知道大家明白吗？这里还有注意的就是：

这里说的左边指的是左子树上的节点的值

比如这里的7，千万别抬杠说“庆哥，庆哥，这个7不是在8的右边吗？不信你看”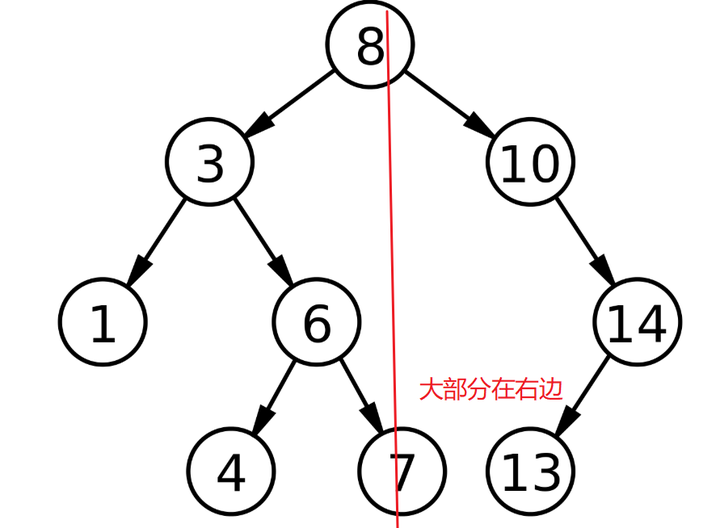

哈哈，千万不要这样想哦。

这就是二叉搜索树了，看定义，我们觉得其实挺好理解的，另外啊，关于二叉搜索树的基本概念，你还需要知道这些：

二叉搜索树，英文名称是：Binary Search Tree，我们一般就简称BST，另外它还有其他的名字，比如二叉排序树，二叉查找树，记住这指的都是一样的，我这里习惯说成二叉搜索树。

最后再总结一下，啥是二叉搜索树：

二叉搜索树是基本的数据结构，是具有以下性质的二叉树，当然也可以是空树：

若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
若任意节点的右子树不空，则右子树上所有节点的值均大于或等于它的根节点的值；
任意节点的左、右子树也分别为二叉查找树；

以上说了这么多，其实目的就一个，让你明白什么是二叉搜索树，它的概念本身比较简单，可能刚接触的话会感觉比较迷糊。

假如说现在你已经掌握了什么是二叉搜索树，那我们接下来看看下一个问题：二叉搜索树的优势在哪？

二叉索树的优势

数据的逻辑机构和物理结构

我们在说二叉搜索树的时候，需要先来回顾一下之前学习关于数据的逻辑结构和物理结构，我们知道，对于数据的存储该选择什么样的数据结构，那就要取决于数据的逻辑结构和物理结构。

所谓数据的逻辑结构指的就是数据之间具有什么样的关系，一般如下：

一对一（采用线性数据结构）
一对多（采用树结构）
多对多（采用图结构）

然后我们还需要知道的是，对于某种数据结构来说，我们实现的方式有两种：

顺序存储（数组）
链式存储（链表）

也就是说啊，当我们确定了要采用树结构了，我们下一个要考虑的问题就是看看这个树结构要采取顺序存储还是链式存储，那这个就要有数据的物理结构来决定了。

所谓的数据的物理结构一般就是指的数据在内存中的存放形式：

集中存放（顺序存储）
分散存放（链式存储）

这些知识，你是需要提前知道的。

二叉搜索树的存储结构

首先既然是树，那肯定存放的是具有一对多关系的数据，这个毋庸置疑的，我们就不需要再去考虑数据的逻辑结构这一块了，也就是说剩下的重点就是要考虑数据结构的存储结构了，也就是看看是采取顺序存储还是链式存储了，当然了，我们这里根据数据的物理结构来判断，可能采取顺序存储，也有可能采取链式存储。

不过这里你要记住了，二叉搜索树通常情况下采用的链式存储，也就是使用链表的形式，那我们就知道了，链表的的话对于更新的操作效率比较高，因为只需要改动相应指针指向即可，不用进行挪动什么的（数组），那么二叉搜索树采用链式存储自然有这个优点：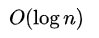

所以，对于二叉搜索树而言，它相比较其他数据结构来说在查找，插入和删除等效率比较高，时间复杂度为

这里可能有人会有疑问了，链表是在更新操作效率比较高，查找的话不应该是数组更快吗？链表的查找需要依次遍历，时间复杂度不是O(n)吗？

确实如此，但是这里在二叉搜索树这块就变了，我们应该还记得二叉搜索树上的节点数据的特点吧，也就是我们上面方分析的，比左边的大，比右边的小，我们查找的时候根节点开始，进行的就是二分查找啊，因为比当前节点小的数都在左边，大的都在右边，而二分查找的时间复杂度为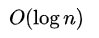

所以在查找这块，二叉搜索树的效率还是可以的。

二叉搜索树相关操作的时间复杂度

然后我们来看下关于二叉搜搜索树的相关操作的时间复杂度，这里有一张图片挺好的，来自维基百科：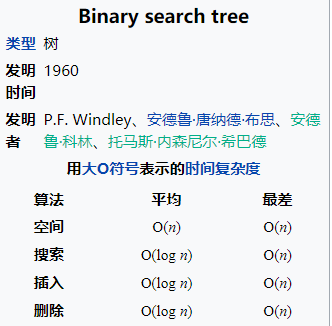

可以看到，对于二叉搜索树的搜索，插入和删除来说，时间复杂度都是

不过这个都是平均，这里还有个最差的情况降低到了O(n)的情况，这是怎么回事呢？我们看下，对于二叉搜索树来说可能有这样的情况：

就是比如有个有序的序列，数据大小一次增大或者增小，就比如上面的数据一次变大，这样实际上就会退化成链表了，这个时候搜索，插入和删除的时间复杂度最差就退化到O(n)了。

那这个时候怎么办呢？这就需要进行优化，也就是需要旋转，像AVL和红黑树就解决了这个问题，就是二叉搜索树的自平衡，这样就可以把最差的时间复杂度也优化到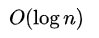

简单小结

到了这里，我们基本上把二叉搜索树一些基本的概念知识点都介绍的差不多了，当然，可能有遗漏，大家可以留言说一下，我后续还会发文进行补充的。

其实吧，我们再讲二叉搜索树的话，接下来就是讲关于二叉搜索树的实现了，也就是二叉搜索树如何实现查找啊，增加和删除啊，重要还有二叉搜索树的遍历等等，这些其实就要涉及代码了，上面说的那些都是停留在二叉搜索树的概念性认识，就是让你了解二叉搜索树，接下的重点就是我们需要自己手动实现一下二叉搜索树，这样你才能真正的理解这个数据结构。

二叉搜索树该如何进行插入操作

就是不会写代码

很多人刚开始学习数据结构的时候，都有这种感觉，我看概念的话觉得都懂了，但是真的让我去实现，自己写代码的话就会感到无从下手。

这其实也是我们学习编程都会遇到的一个问题，就是我看视频或者看书觉得自己都可以看得懂啊，但是让自己写代码的话却写不出来，所以啊，你看的懂和能写出来完全是两码事。

所以啊，平常学习编程一定要多敲代码

很多人在接触链表也就是链式存储这块的时候，会迷惑这个节点咋表示啊，有点抽象啊，还有指针指向，这些看起来比较抽象，用代码？怎么搞啊？

就拿今天说的二叉搜索树来说吧，我们要实现它的很重要的一步就是要确定这个节点怎么表示啊，这个怎么搞啊，有点懵啊，我们先来看画图怎么表示的，比如这里有一个二叉搜索树：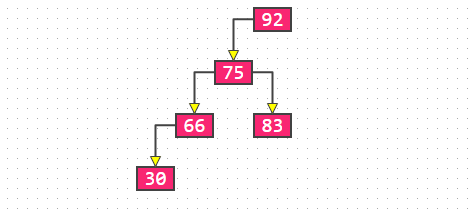

你就比如这个，我们该怎么用代码表示呢？

节点该怎么表示

首先啊，你看，我们直观来看，是不是每个节点是一个数据，然后还有指针指向，就是那些箭头，所以最基本的一个节点包括：

数据元素
箭头（也就是指针，一个节点有两个）

简单来看是不是就是这些，要记住，这是节点包含这些内容，那么这个节点是一个整块的内容，该怎么表示，在java中不就可以使用一个类来表示嘛，也即是这样：

class Node { }

然后就是包含的里面的东西，首先是数据，这个数据这里暂定为整型类型，然后我们在类里面定义这个数据元素：

class Node { int element; }

接下来就是数据指针的表示了，很多人会疑惑这个该怎么表示，你想啊，这个指针指向的不也是个节点嘛，这里的节点已经是个Node对象了，那么一个节点里面保存的指针不就是指向另外一个节点嘛，这不就是保存的另一个对象的引用地址嘛，所以我们可以直接在类里面声明节点对象，也即是这样：

：

class Node { int element; Node left; Node right; Node parent; }

咋样，是不是看明白了，然后这里还需要记录一个父节点，因为后续的插入啥的要根据父节点来操作，然后我们还需要添加构造函数：

class Node { int element; Node left; Node right; Node parent; public Node(int element,Node parent) { this.element = element; this.parent = parent; } }

如此一来，我们就表示了二叉搜索树的节点，接下来就是添加节点的操作。

二叉搜索树添加操作

在此之前，我们需要设定两个参数，一个是代表节点个数，一个是代表根节点：

private int size; private Node root;

这个应该好理解吧，然后就是添加操作：

/** * 添加节点 */ public void add(int element) { //添加第一个节点 if (root == null) { root = new Node(element, null); size++; return; } }

这段代码的逻辑也很简单，你想啊，我们刚开始肯定是个空树，那么你添加的第一个节点理所应当的称为根节点，然后节点个数加一，这个不难理解啊，接下来我们看后续的添加操作：

//添加的不是第一个节点 //找到父节点 Node parent = null; Node node = root; int cmp = 0; //插入的节点与父节点进行比较 while (node != null) { cmp = compare(element, node.element); //向左向右之前保存父节点 parent = node; if (cmp > 0) { node = node.right; } else if (cmp < 0) { node = node.left; } else { //相等 node.element = element; return; } }

这些代码就需要好好说道说道了，不然我真怕有些伙伴看不懂，首先我们先看这个图：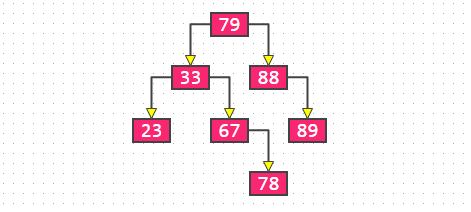

假设这里的根节点79已经添加上去，我们添加第二个节点的时候，是不是需要与根节点的79进行比较，看看是比79大还是小，从而决定该把新插入的第二个节点放在79的左边还是右边，然后目前这个树只有一个根节点79，它是没有父节点的，对应的就是这些代码：

//添加的不是第一个节点 //找到父节点 Node parent = null; Node node = root; int cmp = 0;

这个node就代表当前节点，此时就是根节点啊，这里还定义一个整型变量cmp，主要是后续为了比较两个节点根绝cmp的值来确定两个值的大小。

接下来就是核心代码：（目的就是找到新插入节点的父节点）

//插入的节点与父节点进行比较 while (node != null) { cmp = compare(element, node.element); //向左向右之前保存父节点 parent = node; if (cmp > 0) { node = node.right; } else if (cmp < 0) { node = node.left; } else { //相等 node.element = element; return; } }

继续看这个图：

假如我们要插入一个新的节点，是不是需要先与根节点78比较，看看是大还是小，比较有三种结果，如果是等于的情况，就直接覆盖当前节点的数据值，如果是大于或者小于，那都需要下移，将新插入的节点数据与33或者88比较，而此时的节点（需要与新插入节点比较的那个节点）node就变成了33或者88了，而无论是33还是88,79都是他们的父节点（其实是父节点的数据值，我这里为了叙述方便）。

所以需要把33或者88所在的节点编程当前节点node好与当前节点比较，在此之前需要先记录着父节点，比如这里新增加的节点的数据值比79大，那需要与79的右节点的数据值比较，图上是88，假如这里是空呢？我们是不是就需要把新插入的节点放在88的位置。自然而然，79就是我们插入新的节点的父节点，这就达到了我们的目的。

ps：这里可能没那么好理解，记住核心，你插入新节点，就需要需要当前节点比较，比当前节点大就去与当前节点的右子节点比较，小就去与当前节点的左子节点比较，直到找到左右子节点为空，就是新节点的位置，在此之前也记录了父节点的位置，后续就可以根绝父节点插入新节点了

怕你们不理解

然后这句代码： node = node.right;执行结果node肯定是空，因为我们默认79的右节点是空的，那么这段代码就循环结束，也就进入以下代码：

// 看看插入到父节点的哪个位置 Node newNode = new Node(element, parent); if (cmp > 0) { parent.right = newNode; } else { parent.left = newNode; } size++;

经过上面的步骤，我们找到了新插入节点的父节点，剩下的就是根据是比父节点数据大还是小，然后存放到父节点的左子节点还是右子节点，这个好理解！

然后就是那个比较方法了：

/** * @param e1 * @param e2 * @return 0代表相同，大于0，e1大，否则e2大 */ private int compare(int e1, int e2) { return e1-e2; }

至此，关于二叉搜索树的简单插入就实现了，当然，上述实现肯定有不足之处，比如有些地方需要判空等等，这里只是提供一个思路和简单实现，后续我们会慢慢完善的。

好了，今天的文章就到这里，后续我们会继续探讨二叉搜索树的其他知识，欢迎持续关注！

有相同爱好的可以进来一起讨论哦：企鹅群号：1046795523

学习视频资料：http://www.makeru.com.cn/live/1392_1164.html?s=143793